2004年10月

トップページに戻る谷山浩子さんのページ連絡先 kagami@evariste.que.ne.jp
2004年9月 2004年11月更新履歴と日記の先頭に戻る日記の目次集合論雑記目次
たかたにさん Y.Kumagaiさんはやしさん redcat_mathさん tri_iroさん
Stromdorfさんてなさくさん渕野さんの伯母野山日記
最近のコメント(50件) Twitter (@kagami_hr)

02/25 aiueo 01/01 かがみ 01/01 ゼルプスト殿下 01/01 かがみ 01/01 ゼルプスト殿下 05/10 かがみ

2004年10月31日(日)

アキレスと亀
先日ボールの跳ね返りに関する思いつきを書いたのですが、ちょっと考えてみるとこの論法は「ゼノンの逆理」の考察にも応用出来ると気がつきました。「ゼノンの逆理」は有名でみなさんご存知だと思いますが、いちおう記述しておきますと、
[ゼノンの逆理]
アキレスと亀がかけっこをすることになり、鈍足亀の要望により、亀はアキレスより 10秒前に走り出すことになりました。さて亀が $A_0$ 地点にいるとして、いずれアキレスは $A_0$ 地点に到達します。ところがそのとき亀はほんのちょっと進んでいるはずで、その位置を $A_1$ とすると、アキレスが $A_1$ 地点に到着するのに若干の時間を要することになりますが、そのときやはり亀はちょっとだけ進んでおりまだアキレスは追いつけない。以下 $A_n$ 地点にアキレスが到着した場合、亀はやはり少し前に進んでいるのでアキレスは永久に亀に追いつくことは出来ない。
ということなのです。もうすこし図式的に記述すると、
アキレスが $A_0$ 地点に到達。そのとき亀は $A_0~+~p_0$ 地点まで到達
アキレスが $A_1~=~A_0~+~p_0$ 地点に到達。そのとき亀は $A_1~+~p_1$ 地点まで到達
...
アキレスが $A_n~=~A_{n-1}~+~p_{n-1}$ 地点に到達。そのとき亀は $A_{n}~+~p_{n}$ 地点まで到達
...
という感じです。もちろん上記は全然逆理ではなく、亀の速度ががアキレスより遅いと仮定すれば、
$\sum_{n=0}^{\infty}{p_n}$
が収束し、アキレスは有限の時間(速度が一定ならば移動時間は距離に比例) で亀の位置に「到達」出来るのです。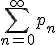
せっかくなので具体例で計算しますと、亀ではあんまりのろすぎて計算しにくいので、アキレスと私が競争したと仮定します。アキレスは 10m/s の速さで、私はまあ 5m/sec ということにします。そして私が 10秒前にスタートするということで。まず普通の計算で何秒後に追いつかれるかと言いますと、これは小学生の問題で、(アキレスがスタートしてから)10秒後ということがすぐに分ります。それではさっきの論法で $A_0~=~0$ をスタート位置とすると、アキレスがこの位置に「到達する」のは、スタートが 10 秒遅れなので 10秒後と考えて良く、その時の私の位置は $A_1~=~A_0~+~50~=~50.$ 以下同様に
$A_2~=~A_1~+~50/2\cr~A_3~=~A_2~+~50/4\cr~\cdots\cr~A_n~=~A_{n-1}~+~50/2^{n-1}\cr~\cdots$
すると
$\sum_{n=0}^{\infty}{p_n}~=~50~\sum_{n=0}^{\infty}{1/2^n}~=~100$
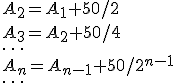
となり、私が 100メートル走ったところで貯金を使い果たし、アキレススタート後 10秒後に追いつかれることが、こちらの計算でも確認出来るのでありました。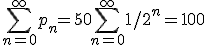
余談ですが、たまに 0.99999... は 1 にならないと主張する「とんでも君」がいたりしますが、その人の論法を信じると「アキレスは本当に亀に追いつけない」ということになります。

2004年10月30日(土)

表彰式
今日は第３５回藤沢市総合かがく展の優秀作品の表彰式ということで、モカ・奥さま・私三人で、こちらに出かけまして、表彰状と記念品をもらい、さらに姫は受賞作品の内容や苦労話に関するスピーチを行いました。とても良いスピーチでした。

本当は式というのはあんまり得意ではないのですが、こういう場合はなかなか気分が良いものです。まさに親ばかです！！。さらにモカの学校の担任の先生もわざわざ来て下さりまして、みんなで写真を撮ったりしたのです。式に行ったついでに、色々作品を見てきたのですが、力作・労作が沢山展示されており、聞いたところによりますと、最優秀を決めるときも審査の先生方がかなり苦労されたのこと。上の方のレヴェルでの優劣の評価に関しては運の要素もかなりあることを痛感したのであります。式終了後ファミレスで食事して帰宅。

2004年10月29日(金)

まわし
とつぜん子供から質問が...。
パパー、相撲でまわしがほどけたら反則負けでしょ。それなら相手のまわしをほどく技ってないの〜(^^。
さすがに私の娘！！。なかなか鋭い観点で物事を考えます。それにしても親子の血は争えないもので、実は私も小さい頃父親におんなじことを聞いて、「下らんことを考えてるんじゃない」と怒られたことがあったりします。
ところが上記重大なる疑問に関しての半公式見解が、相撲協会と密接なる関係がある「大相撲」(「相撲」だったかも知れない)という雑誌に掲載されたことがあるのです。30年程前のことなのですが、読者の質問コーナーでおんなじ様な質問がありまして、回答としては、
- そもそもそんな馬鹿なことを考える相撲取りがいるわけがない。
- よしんばそのような不心得者がいたとしても、まわしは非常にきつくしめられているので、相手のをほどこうとしている間に自分が負けてしまう。
という感じのものだったのです。うーむ、いまいちつまんないですねー(^^。それよりも面白かったのは、こちらも大分昔の話で、テレビで夜の 7時半から毎日 15分くらいやっていたクイズ番組があったと記憶しているのですが(名前を覚えている人がいたら教えて下さい)、その中での事件なのです。クイズの問題が、
相撲には技でない決まり手が二つあります、一つは「勇み足」ですがもう一つは何でしょう。
というものでして、問題の意図としては、自滅してしまう負け方は何かということで、正解は「腰くだけ」なのです。ところがやっぱり面白いこと考えちゃう人っているもので、
- ぴんぽーん ←回答ボタンを押した音
- 山田さん(仮名)どうぞ ←アナウンサー
- 笑いをこらえながら、「まっ、まっ、まわしがほどけたとき」 ← 山田さん
- ブー ←不正解
- うっうぷっ...え〜〜正解は「腰くだけ」です ←アナウンサー
なる事態に陥りまして、いやはや他の回答者は大笑いしているし、山田さんはとっても恥ずかしそうな表情になり、さらにアナウンサーも笑いをこらえるのに必死の様子で、もちろん私もテレビの前で大笑いしていたのです。
ところで、まわしがほどけるといえば「ゆるふん」です。最近は相撲を見ることもほとんどなくなったので、断言は出来ないのですが、昔に比べると「太りすぎ」の力士が増えた割には、露骨な「ゆるふん」力士は減ってきたような気がします。一昔前「ゆるふん」を武器として横綱まで上りつめた力士としては、輪島・三重の海・旭富士あたりが代表だと思うのですが、本当にほどけそうになる場面も多く、はらはらどきどきわくわく感があったような気がします(^^。最近はそのようなことも少なくなったのが相撲人気の凋落傾向に拍車をかけているのかも知れません(←おおうそ)。

2004年10月28日(木)

ぼったくり
私が勤めている会社では、5年ほど前に購入した、すでに保証期限切れの Dell の高級サーバー(すごく高かったそうな...)を業務用のデーターベースサーバーとして使用しているのですが、数日前からハードウエアー異常検出ランプが灯るようになったのです。
そこで担当の人が Dell のサポートに連絡したところ、ブート可能な診断フロッピーを作成する EXE ファイルが送られてきまして、フロッピー自体は簡単に作ることが出来たのです。ところがそれをサーバーに挿入して電源を入れたのですが...
フロッピーディスクを読み込むことが出来ません(-_-)
肝心のブートデバイスが壊れてしまったのでは、原因を調べるのは不可能です。ただし普段アクセスしていないフロッピーの故障を自動検知するとも思えないので、異常検出ランプ点灯の原因は他にありそうです。
てなこと考えながらフロッピーを「むにむに」しながら何回かブートを試みたところ、一回だけ運良くブートしたのです。どうも長年使っていなかったので、ごみがたまっていたようです。というわけでフロッピーに書き込まれた診断ファイルなるものをサポートに送ったところ、背面のファンの回転数が下がっているとのこと。「なんだファンなら送ってもらって交換すれば数千円で済むな〜」ということで見積りを依頼したのですが、Dell の回答は、
部品だけをお送りすることは出来ません。技術員出張で６万うん千円頂きます(-_-)
とのことなのです。それは高すぎるのでは、と色々交渉したのですが、ファン自体に特殊なネジを使用しているそうで、普通の工具では交換が不可能らしく、とにかく部品のみの発注は出来ないそうなのです。
うーむ、どうも特殊なネジを使っているあたり、あえて普通の人が交換出来ないようにするための仕掛けの様に思えるし、本音としては保証期限が過ぎた PC など使用せずに新しいのを購入しなさい、ということだと思うのですが、なんともはや、保証期限が切れたとたん「ぼったくり」モード突入の印象は否めません。個人的にはやたら高いサーバー様を置いとくよりも、普通のマシン２台体制で運用した方が、コスト的にも安定性からみても得だと思うのですが、いまさらシステムを新しくするのも大変そうだし、マシンを新規購入しない限り、高いお金を払い続けることになりそうな予感がします。

2004年10月27日(水)

モカちゃん一等賞をとる
今、藤沢市教育委員会主催の第３５回藤沢市総合かがく展というものが開催されているのです。その中のコーナーで、
市内小中学校の児童生徒および市民の理科研究作品約１４００点の展示
というものがありまして、市内各小中学校の夏休み理科自由研究の中から優れた作品を選ぶのでが、やったーやりました〜！！。モカちゃんが
小学生の部最優秀賞(^^)
を受賞したのです。

姫のお題は「うずまき」で、内容は「アサガオのつる」と「水のうず」に関する観察・考察なのです。もともと北半球と南半球のアサガオのつるの巻く向きが逆になるのでは、という誤った仮説から始めた研究なのですが、身近に発生するうずが「コリオリの力」に関連しているのか、という風にテーマを一般化したのです。実際台風の渦に関しては、コリオリの力により、北半球と南半球により向きが変わるのですが、モカちゃんの結論としましては、アサガオのつるの向きや、お風呂の排水口から流れでる水の渦の向きの様な、地球規模に対して小さな現象に関しては、コリオリの力は関与しないことが推測されるということだったのです。
もちろんアサガオのつるの向きに関しては、南半球まで調べに行くことは出来ないので、教えて頂いた知識や、逆さアサガオの考察による推測です。また身近に発生する渦巻に関しては、お風呂で何回も実験を行い、左右両方の向きの渦が発生したということからの推測なのです。さらにこの実験により、渦が大きいほど単位時間あたりに水の流れる量は少なくなる、という推測も得られまして、この事実に関する考察としては、「200 回の実験を行い、渦が大きいほど中心部で水が流れていない部分の断面積が大きいことを観察した。従って実際に水が流れる部分の断面積が減少する」ということだったのです。
本人もとても喜んでおります。アサガオについて貴重な助言を下さった方々に改めて感謝いたします(^^。

2004年10月26日(火)

ボールは止まる・止まらない？
今日は案外真面目な問題。
1 メートルの高さからボールを落としたとして、このボールは 0.9メートルの高さまで跳ね返るとします。2回目は 0.9x0.9 = 0.81メートルまで、3回目は 0.9x0.9x0.9=0.729メートルまで跳ね返るわけです。さて問題。
このボールはしばらくすると一見静止状態となりますが、本当に静止するのでしょうか。それとも跳ね返りが余りに小さくなり静止しているように見えるだけで、本当は永久に動き続けるのでしょうか。ただし理想的なニュートン力学の状況を仮定し、量子論的なゆらぎ、その他ボールの材質等の原子論的な「ごたごた」は考えないこととします。さらにボールが上昇した場合(地球から離れるので)若干引力が減少するのも無視します。
この問題は昨日の帰りの電車で思いついて解いてみたものなのですが、計算自体はそんなに難しくありません。まず自明なこととしては、
n 回目の跳ね返る高さは 0.9ⁿ メートルなので無限回跳ね返る
ということです。それでは「無限回」の跳ね返りに必要な時間を計算してみましょう。一般に初速度 $v$ で地上から跳ね返ったボールの速度が 0 になる(つまり最高の高さまで上がる)のに経過する時間 $t$ は、ボールが重力加速度 $g$ でひっぱられるということで
$t~=~v/g~\qquad~~{\rm~(a)}$
となります。またそのときの初速度と最大高さ $h$ の関係は運動エネルギーと位置エネルギーの関係 ${{1}\over{2}}~{mv^2~=~mgh}$ により、
$v~=~\sqrt{2gh}~\qquad~{\rm~(b)}$
(a)(b) から $v$ を消去すると、跳ね上がってから最高の高さまで上がるのに必要な時間は、高さの関数として、
${\large~t}~{\large~=}~\sqrt{{\large~2h}\over{\large~g}}$
と表されます。最初の問題で 0.9 と書いたのを一般に(弾性率というのかな...) $\alpha$ で表すと、ボールが振動する時間の合計は、
$\sqrt{{\large~2}\over{\large~g}}~+~~2~{\large~\sum_{n=1}^{\infty}\sqrt{{\large~2~\alpha^n}\over{\large~g}}}$
となります。最初の項は一回目に落っこちる部分で、以降は上がって落ちるので無限級数全体を 2 倍しているのであります。ところがうれしいことに、上記無限級数の項は公比 $\sqrt{\alpha}$ の等比級数となるので、 $\alpha~<~1~$ ならば収束します！！。というわけでちょっと計算するとボールが動いている累計の時間は、
$\sqrt{{\large~2}\over{\large~g}}~{(\Large~{{1+\sqrt{\alpha}}\over{1-\sqrt{\alpha}}})}$
となり $\alpha~=~0.9$ の場合 17.1 秒後に無限回振動して完全に停止するのでした。
＃累計時間が収束することは間違いないと思いますが、細かい計算は間違っているかも。
＃そもそも 17.1 秒って少し大きすぎるような気ももするし...。
＃変なところがあったら教えて下さい。
↑
地球物理学の博士から「間違ってなさそう」というお墨つきを頂きました(^^。

2004年10月25日(月)

完全に限界ご家族さま PC
ご家族さまが使用している PC は 3年以上前に購入した Celeron 600MHz 程度の激とろものなのですが、最近はもともと遅いのを差し引いても、使用に耐えない状況になってきたようです。症状としては、
1. 起動して使用可能になるまで 5分くらい時間がかかる。
2. 起動中にリブートする場合がある。この場合 1 の条件があるので使用可能になるまで 10分もかかる。
3. 起動したままユーザーの変更を行うとシャットダウン中に固まる。
4. 先日奥さまのブラウザのブックマークが突然消滅した。
5. 先日長女のブラウザのブックマークが突然消滅した。
6. 先日二女のブラウザのブックマークが突然消滅した。
7. 先日モカちゃんのブラウザのブックマークが突然消滅した。
あたりでして、特に 2番目の症状に関してははハード不良の疑いもあるのですが、新しいのを買うお金もないので、とりあえず次の土日あたりに、二年近く放置した Windows2000 の再インストールをやってみるのが良さそうです。奥さまや子供達の話を聞くと、メール・ブックマーク・その他少々のデータ以外は置いてないそうなので、バックアップは比較的楽そうです。ただし全員何をどこに置いたかを把握していないので、調査する必要があるのと、バックアップ忘れがない様にに注意しなければいけません。
＃そういや二女とモカがユーザー辞書とか言ってた。
＃どうやってバックアップするのだろう(^^。

2004年10月24日(日)

一夜漬け
実は明日会社で財務に関する研修会というものがありまして、まあ言葉くらいは知っとかないといけないかな〜、ということで参加希望をしてあるのです。ところが、お話聞いていれば良いのだろうと思っていたのが甘い考えで、なんか本格的な講師がきて下さるそうで、さらに
予習用の宿題が出ている
のでした(^^。講習の担当の方は本当に一生懸命準備をして下さっているので、あんまりいいかげんな態度で参加するわけにもいきません。なので、本来はもっと前から勉強しておかなければいけなかったのですが、とにかく何も予習しないで失礼があっては大変なので、本日一夜漬けの勉強だったりするのです。
こういうお金がらみの勉強は生まれて初めてなのですが、本当に難しいです。例えば「資本金」とかの意味もいまいち分らないし、良識のある親ならば、借金は「良くないこと」であると子供に教えると思うのですが、どうも企業の場合はそうでないらしく、企業のお金というのは一般の常識とは異なる動きをするようで、謎は深まるばかりだったりするのでした(^^。

2004年10月23日(土)

避難訓練
今日、新潟県で大きな地震がありましたが、数日前モカちゃんの学校で避難訓練があったなのです。ところが、その日は丁度当時担任の先生がお休みで、子供達だけで校庭に避難するということになってしまい、その結果先生が誘導するよりは若干の遅れが発生し、結局全学年で一番遅くなり、姫のクラスのみがもう一度教室に戻り避難のやり直しになったのです。
問題はその後でして、次の授業を行った先生が、「あなたたちが遅いから授業の時間が短くなってしまった」ということで、色々文句を言い始めたのです。この先生は今年からモカの学校に転任してきた人で、あまり評判が良くなく、モカは相手が大人でも良くないことははっきりと言うので(私もしょっちゅうおこられている...)、この件に関しても「私達は先生がいないのに自分達だけで一生懸命避難した」と発言したそうなのですが、その後も先生はいろいろ文句を言い続けて、非常に険悪な状態になったそうなのです。さらに、丁度そのとき校長先生が通りかかり、「みんな一生懸命避難したのだから」とその場をおさめようとしたのに、先生は納得せず延々と文句を言い続けたのです。
もちろん校長先生としては、担任の先生がお休みとはいえ、避難訓練で誰も誘導しなかったのはまずいと認識されていたと思うのですが、その先生はそのようなことを理解する能力を全く持たないようです。本当に避難が必要な事態に陥った場合、運悪くこの先生の授業中であったりするとさらなる混乱が予想されます。そのような運の悪い事態にはなって欲しくないのですが、もっと根本的な問題として、一人だめな先生が他校に転出すると、必ず別のだめな先生が転入してくる(もちろん学校間でトレードしているのです)、という悪循環をなんとかして欲しいものです。

2004年10月22日(金)

ピン配置ではまる
ちょっと前まで VHDL にて FPGA がらみの開発を行っていたのですが、今日はお客さまから具体的なピンの配置図を頂きまして、それを元に定義ファイルを作ったのです。ところがこれが予想以上に大変なのです。まずピン配置図が PDF 形式でコピペ出来ないし、印刷すると字が小さくて私の視力では読めないのです(^^。
というわけで PDF のファイルを PC 上で拡大して定義ファイルを作り始めたのですが、ピンが 300本以上あるので、とってもとっても面倒なのです。さらに例えばデーターバスなど、VHDL 言語上では
SIGNAL D:std_logic_vector(31 DOWNTO 0)
という風に記述出来るのですが、実際のピン定義ファイル上では、
```
D[31]  H13  ← H13 というのがピンの位置を表す
D[30]  L14
D[29]  L13
D[28]  J16
...
```
の様に一本ずつ具体的に記述する必要があり、抽象的にはデーターバス 32本を一つのものと考えて良いのに、あたりまえとはいえ規則性がないのを絵を見ていちいち書かにゃあかんのです。それにしてもこんなのが 300以上ですよ。さんびゃく以上！！。
結局 15本位書いたところで精根つき果て(おい^^)、読み上げの応援をお願いすることになったのです。お願いした方はいつも親切にしてくださる H さんでして、いやはや本当に面倒な作業なのに、いやな顔もせずに正確に読み上げて下さり、どうもありがとうございました。ちなみに H 氏は愛知県出身の熱烈なる中日ファンでして、今日は西武球場まで日本シリーズを観戦しに行かれたはずなのですが、結果を見ますと中日が快勝したようで、まあ人助けをしたご利益があったということでしょうか(^^。

2004年10月21日(木)

お財布を忘れる
今朝は奥さまに駅まで車で送ってもらったのですが、車から降りて改札で定期を出そうとしたら、
お財布がありません(-_-)
むむむっ、これはなんというまぬけな...。さらにおうちの鍵もしっかり忘れていたのです。実は前にもこんなことがありて、そのときは駅前の交番に駆け込んで「明日必ず返しますから、会社にたどりつく 600円だけ貸して下さい」とお願いしたことがあるのですが、そういうことは出来ないということだったので、こちらは頼りになりません(＊)。最大の問題は鍵を忘れたということで、タクシーに乗ったり、30 分くらい歩いて帰ったとして、奥さまがそのままどこかにおでかけで、おうちに誰もいない場合路頭に迷うことになるのです。この場合モカちゃんの小学校に行って鍵をもらう、という作戦も考えられないではないのですが、いくらなんでも逆の状況ならともかく、親が子供に鍵をもらいにゆくというのも、とっても恥ずかしい事態だと思うのです(^^。
てなこと考えながら、何回かおうちに電話をかけたところ、運良く奥さまが出て下さりまして、結局もう一度車を出してもらって、駅までお財布と鍵を持ってきてもらったのです。いやはや、それにしても普段はぎりぎりまで寝てて、あわてて会社にゆくという毎日なのですが、今日は比較的早起きをしまして、のんびり朝食を食べたりしていたのですが、こういうときに限って忘れ物をするんですね。今度から気をつけないと...。
(＊) 当時は携帯とか PHS 持っていなかったので、頼み込んで電話代の 10円だけ貸しもらい、ちゃんと次の日返したのでした。

2004年10月20日(水)

くるくる電車
今朝奥さまと、通勤電車ってとっても込んでるからいやだね〜、という話題になったのです。そもそもあんなに間隔が空いているのだから、もっと電車を増やせば良いのではと思うのですが、諸般の事情ありて今以上に増やすのは困難なのなのかな、などと話をしているまさにその時に、素晴らしい理論を考えついたのでした。
電車と電車の間にすき間があるから良くないのであり、全部繋げて一本の電車にすれば良い(^^。
むむむむむっ、これは本当にすばらしい！！人類の歴史上最も偉大かつ完璧なる理論ですな。ということで奥さまに話をしたのですが、奥さまのご意見としては、「例えば新宿と藤沢を全部電車でつないだら動きがとれなくなるじゃない」ということなのです。しかしながら、もちろんそんなことは事前に考えてありまして、この問題を解決するためには、上りと下りの線路を繋いで環状にして、長大な電車をくるくる回せばよいのです。ところがさらに奥さまの疑惑は続き、「どうやって降りるのよ。例えばある場所に座っていたとして、停車したら丁度駅と駅の真中だったら困るじゃない」ということなのです。ふふふふふっ、私の理論をあなどるなかれ...
駅も全部繋いでしまえば良いのだ〜(^^
そもそも今回の大発見は、東京駅で新幹線に乗る場合とか、ディズニーランド方面に行く場合、かなりの距離を歩かなければならないのに、おんなじ駅の中だとあんまり歩いた気がしない、という心理学的(つまり医学的)観点も十分考慮してあるのでして、その様な観点からみても究極の物理・医学理論なのです。
いずれにしても、自分が考えたということを値引いても、これほど完璧なる論理の裏づけがある理論は今まで存在しなかったことは間違いありません。というわけで、この業績により、史上初のノーベル物理学・医学生理学賞同時受賞は間違いないと思うのでありますが、やっぱりだめかな...(^^。
＃奥さまに「そんなら長い高速エスカレーターみたいなの作ってもおんなじじゃない」
＃とつっこまれて、うーむと考え込んでしまったのは内緒なのです。

2004年10月19日(火)

モカちゃんぱどタウンにはまる
なんかご家族さま用 PC の前で姫が一生懸命書き込みしているので、なにかな〜と思って覗いたところ、「絶対みちゃだめ〜」ということなのです。そこで、「見ないから何やってるか教えて」と聞いたところ、ぱどタウンにおうちをこしらえて、お友達とチャットとか色々やっているそうな。どうも同級生に誰かいいだしっぺがいて、参加している子もかなり多いらしいのです。いやはや、こういうのがあるという噂は聞いていましたが、モカちゃんもしっかりはまっていたとは知りませんでした。
さらに、姫にはあんまり関係ないらしいのですが、不快な書き込み等のトラブルもいくつか発生し、親が先生の所に苦情を持ち込んだ例もあるそうな。私の感覚ですと、これは学校外での当事者同士の問題なので、先生に苦情を持ち込むのは筋違いだと思うのですが、奥さまの意見によりますと、「親同士が直接談判するとかえってこじれるので、間に先生を通した方が良い場合が多い」そうな。うーむ、小学校の先生も仮想の世界でのいざこざまで持ち込まれるとは、なかなか大変なご時世になったものです。
＃ちと探索したけど姫の家らしきものは発見できず(^^。

2004年10月18日(月)

LUMIX の SD カード転送速度
確かに遅いです(^^。LUMIX の USB インターフェースをカメラと PC 直結で使用すると、体感的に SD カードリーダーから読み取る 5倍程度時間がかかる感じはしていたのですが、ちゃんと計測してもその通りなのですね。まあこのあたりはほとんど意味なく一緒に付いてくる 8M バイト程度の SD カードとおんなじで、単なるおまけと考えた方が良く、いまいち実用性に欠けることは事実のようです。ただしおまけの SD カードが全く役に立たないのに反して、USB インターフェースの方は、外に出ているとき PC に写真をアップロードしたくなった場合等、少しは役にたつ面もあったりします(^^。撮った写真を SD カードに書く部分は、速度が命なので、ほとんどハードウエアの制御と DMA 転送にて行われるのに対し、SD カードから USB 経由の部分はあんまり速くない CPU による I/O 転送なのかも知れません。

2004年10月17日(日)

一回休み

2004年10月16日(土)

Firefox-1.0 インストール
Firefox-1.0PR がなかなか FreeBSD の ports に反映されていなかったのと、たまに落ちる(＊)以外は不都合もなかったので firefox-0.9.3 のまま放置してあったのですが、やっとヴァージョン 1.0PR が ports に反映されたようなのでさっそくインストールしました。ついでに依存する環境も綺麗にした方が良いあろうということで、
# /usr/local/sbin/portupgrade -R firefox-0.9.3_1
なるコマンドを実行したところ、色々依存する ports がアップデートされた後、めでたくfirefox-1.0.1.p_2 なる ports がインストールされたのでした。ところでこういう大きなプロジェクトの場合内容のことは置いといて、 Makefile がすごいな〜、といつも思いまして、特に FreeBSD の make world なんて神技としか思えません(^^。
肝心の使い勝手なのですが、まあ今までとあんまり変わらないというか...。ただし割りと良く遊びにゆく所で、そのたびに firefox が落っこちるサイトさまがあったのですが、そちらは大丈夫になったようです。
(＊) おそらくたまに落ちる原因は Firefox の本体が原因ではなく Flash 関連のプラグインが原因と思われます。

2004年10月15日(金)

日食予定
昨日「皆既日蝕を見る機会なんて一生ないだろうな」と書いたら、 H さんからつっこみがありまして、2012年5月21日に東京で金環食が見れるそうな。さらに 2035年には本当の皆既日食がこれまた東京で見えるということなのです。まあ 2035年はもう生きてないと思うのですが、2012年はよほど運が悪くなければ生きているような気がします(^^。ところでもちろん一番問題なのはお天気でして、こんなに正確なことが分るのならば 2012年のお天気なんて簡単に分るよね〜、と言ったところ、こちらは非常に難しいとのこと(←あたりまえ^^)。そもそも、日食が滅多に起きないのは、もちろん月の軌道と太陽の軌道がちょっとずれているからでして、日食を多くするために太陽を動かすのは大変そうなので、月を動かすことを目標とすると、
- 月に大量の土砂を持ち込み月を大きくする。
- 月の軌道をなんとかして太陽の軌道に合わせる。
- 月と地球の距離をなんとかして現行の半分位にする。
などが考えられるのですが、こちらも H さんの説によるとなかなか難しいとのことでして、H さんは私の偉大なるアイディアを次から次へと否定するのです。うーむ、どこが悪いのだろうか。確かに、最後の案は万が一失敗して月が地球に落っこちてくると困ったことになるのは分るのですが...(^^。

2004年10月14日(木)

有理整数の意味
例えば昨日の記事のように、この日記では通常「整数」と呼ばれているもの ${\large~(\cdots,-3,-2,-1,0,1,2,3,\cdots)}$ を「有理整数」と書くことが多いのですが、一応意味を書いときます。実は数学の世界では通常の整数のみを「整数」と呼ぶのではなく、方程式、
${\large~x^n~+~a_{n-1}x^{n-1}~+~\cdots~+~a_1~x~+~a_0~=~0}$
の解(ただし ${\large~a_{n-1},a_{n-2}~\cdots,~a_1,a_0}$ はすべて「普通の整数」)のことも整数と呼ぶ場合が多いのです。最高次の係数が 1 であることが重要です。例えば意外に思われるかも知れませんが、
${\large~\sqrt{2}}\cr~{\large~{1+\sqrt{3}i}}\over{\large~2}$
はそれぞれ
${\large~x^2~-2~=0}\cr~{\large~x^2~-~x~+~1~=0}$
の解になるので「整数」なのです。それにしても $\sqrt{2}$ や ${\large~{1+\sqrt{3}i}}\over{\large~2}$ が整数だなんて中学や高校のテストで回答したら×になってしまいますね(^^。この様に整数の意味を拡張したのはガウス(C.F.Gauss)の数論研究に始まり、それ以来整数の研究に対する非常に強力な概念となったのです。というわけで、この日記では普通の整数ということを強調するために「有理整数」なる言葉を多用しているのであります。ついでですが、有理数で拡張された整数になるのは、普通の整数だけです。例えば ${\large~1}\over{\large~3}$ は ${\large~3x-1=0}$ の解であり、この方程式の最高次の項は 1 ではありません。
日食見えず
理由は良く分らないのですが、昨晩 11時半頃に寝たら、早朝 2時頃目が覚めてしまったのです。さらになかなか寝つけなくて、とうとう朝の 4 時半頃になり(この間に昨日の日記を書いたりしていた)、もしこのまま寝てしまったら絶対に朝起きれない、ということで結局半分徹夜のような状態で定時より一時間も前に出社したのです。そういうことで今日はとっても眠いのですが、仕事しないわけにもゆかないので、ぼちぼちやってます(^^。ところで早朝に空を見たところ、もうオリオン座やシリウスの季節なのですね。季節の移り変わりは速いものです。でもお昼前は曇っていて部分日食を見ることは出来なかったのでした。皆既日食を見る機会なんて一生ないだろうな。残念！！

2004年10月13日(水)

比と有理数
モカちゃんが勉強している算数のテキストををみてたら、今は「比とその値」らしきものをやっている様なのです。それにしてもいつも思うのですが、小学生の算数あなどるなかれ。「比」という概念って分りにくいですね(^^。ちょいと引用致しますと、
$B$ に対する $A$ の割合を $A\,:\,B$ と書き $A$ と $B$ の比と呼ぶ
ということだそうで、さらに
$A$ を $B$ で割った値を比の値と呼ぶ
そうなのです。まあこんなことは誰でも知っている当り前のことなのでしょうが、これを眺めていて、そういえば比というは有理数を構成する中間段階で出てくるな〜、と思ったのが本日のお題なのです。
数学を勉強したことある人以外には余り知られていないと思うのですが、(有理)整数の概念は分っているものとして、通常有理数は次の様に「作られ」ます。まず(有理)整数(...-3,-2,-1,0,1,2,...)全体の集合を ${\bf~Z}$ としまして
$A~=~\{(a,b)\,|\,a\in{\bf~Z}\,\wedge\,b\in{\bf~Z}\,\wedge\,b\neq{0}\}$
なる集合を考えるのです。そして $A$ 上の同値関係 $\sim$ を
$(a,b)\sim{(c,d)}\,\leftrightarrow~ad~=~bc$
にて定義し $\sim$ に関する商集合
${\bf~Q}=A/\sim$
を考えると、これがめでたく有理数全体の集合となるわけです。こんな準備をして、小学校のテキストの定義を見直すと、 $a:b$ を $(a,b)$ のことと思えば、 $A$ が丁度「比」全体の集合になっているのですね。うーん、これは初めて気が付きました。さらに「比の値」は同値関係 $\sim$ に関する $A$ から ${\bf~Q}$ への標準写像 $\pi:A~\rightarrow~{\bf~Q}$ による像として定義出来るのです。これは勉強になりました！！実はさっきまで「比」と「有理数」はおんなじものだと思っていたりしたのですが、それは間違いで、「比の値」と「有理数」がおんなじものなのでした。ちょっと具体的に実例を挙げますと、
比 $3:4$ と $6:8$ は違うもの。しかし前記の二つの比の「値」 $3/4~=~6/8$ は同じものである。
ということなのかな。いやはや、それにしても小学校の算数のテキストというものも、ちょっと読んでみると、つっこみどころ満載であると再認識したのでありました(^^。
余談ですが、昔 $0:1$ や $1:0$ は意味があるのか、という議論になったことがあるのですが、 $0:1$ の値は $0/1~=~0$ なので意味があるが $1:0$ の「値」は $1/0$ なので無意味であるというというのが、私の見解だったのでして、この考えは今でも変わっていません。

2004年10月12日(火)

いもむしくん
今朝、通勤の電車に乗ったらなんか首のあたりがむずむずと。どうしたのだろう、と思って手をやったら、
なんかむにゅっとした感触が...
こここっ、こっ、これはいもむしくん！！。わーーー、私こういうのだめなの。たすけて〜〜〜(^^。というわけで何とか手で払いのけたのですが、電車の床に落ちたはずのいもむしくんを見る勇気もなく、さらにじたばたしてたので、回りの人達からは不審の目で見られるし、いやはや連休明け早々とんだ災難だったのでした。さらにその顛末を奥さまにメールしたところ、
> むにゅっとした感触が(^^ ← これが私書いた部分。
いもむし、かわいそう・・・
いもむしだって、変なところに落っこちていい気はしてないはずです。
なんていう返事が来たりして、全く同情してもらえないというダブルパンチだったのであります。余談ですが、モカの運動会の日も、背中にいもむしくんがかなり長時間くっついていたそうで、これは他のうちの子のおかあさんが見つけてくれて、ありがたくも払ってくれたのですが (これも恐くて見れなかったし大声上げてじたばたしたので笑われたし...)、もしかして今年はいもむしの当たり年なの？やだやだそれだけはご勘弁を(^^。

2004年10月11日(月)

モカちゃんリュックを買う
モカちゃんが二三ヶ月前から「もうランドセルはやだ！！」と言い出しまして、話を聞いてみると、今やクラスでランドセル通学してるのは、モカちゃん含めて三人だけなそうな。ということで今日は奥さまとモカ姫と通学用のリュックを買いに行ってきたのです。買いに行って悩んだのは、大きめのでさらにちょっと高いのを買って、中学校に行ってからも継続して使用する予定とするか、これから一年半位しか使わないと割り切って、そんなに大きくなく安いのを買うべきかなのですが、お店をいくつか見たところ安くて使い易そうなのがあったので、割とちっちゃいのを購入しました。さて残り二人のランドセル組は今後どのような行動に出るのでしょうか。ちょっと興味があったりします(^^。いずれにしても、約十四年に渡り三代続いた我が家のランドセル生活も終演となりました。

2004年10月10日(日)

正則の公理
[集合論雑記目次]
本日は「正則の公理」の導入により前回定義した ${\rm~V}$ が集合全体を要素とすることを証明します。その前にまず「推移的集合 (transitive set)」に関するいくつかの簡単な性質を列挙します。推移的集合の定義を思い出しますと、
集合 $X$ が推移的であるとは $\forall{y}\forall{x}(y~\in~X~\wedge~x\in~y~\rightarrow~x~\in~X)$ が成立すること
でありました。 $\forall{y}(~y~\in~X~\rightarrow~y~\subset~X)$ と言っても同じことです。次の事実の証明は容易です。
(a) $X$ が推移的なとき $\bigcup{X},\,\wp(X)$ も推移的
(b) 任意の集合に対してそれを部分集合とする最小の推移的集合が存在する
(a) が成立することは定義よりすぐに分ります。(b) の証明ですが集合 $X$ に対し次の列と ${\rm~tc}(X)$ を帰納的に定義します。
$X_0~=~X\cr~X_{n+1}~=~\bigcup{X_n}\quad(n~\in~\omega)\cr$
そして
${\rm~tc}(X)~=~\bigcup_{n\in\omega}X_n$
すると ${\rm~tc}(X)$ は $X$ を部分集合とする最小の推移的集合となります。まず ${\rm~tc}(X)$ が推移的集合であることは $y\in{X_n}$ とすると $y\subset{X_{n+1}}$ が成立することにより導かれるます。さらに $X\subset{Y}$ 推移的集合とすると、帰納的に $X_{n}~\subset~{Y}\quad(n~\in~\omega)$ が導かれるので ${\rm~tc}(X)\subset{Y}\,.$ ${\rm~tc}(X)$ を $X$ の推移的閉包と呼びます。さて次に ${\rm~V}_\alpha$ に関する簡単な性質を列挙します。
(c) $\alpha~\leq~\beta~\rightarrow~{\rm~V}_\alpha~\subset~{\rm~V_\beta}$
(d) $\alpha\in{\rm~Ord}~\rightarrow~{\rm~V}_\alpha$ は推移的.
(e) $\alpha\in{\rm~Ord}~\rightarrow~\alpha\in{{\rm~V}_{\alpha+1}}$
(c) (d) は ${\rm~V}_\alpha$ の定義と推移的集合の性質と (a) から超限帰納法により導かれます。 (e) の証明も超限帰納法で行われます。即ち $\beta~<~\alpha~\rightarrow~\beta\in{{\rm~V}_{\beta~+~1}}$ が成立していたと仮定すると $\alpha~\subset~{\rm~V}_{\alpha}$ が導かれるので $\alpha~\in~{\rm~V}_{\alpha+1}$ 。さてここで重様な概念を定義します。
[集合の階数(rank)の定義]
$x~\in~{\rm~V}$ とするとき $x~\in~{\rm~V_\beta}$ となる最小の $\beta$ は明らかに極限数ではありません。したがって $x$ の階数(rank) を次のように定義します。
$x~\in~{\rm~V}$ のとき $x~\in~{\rm~V}_{\alpha~+~1}$ なる最小の順序数 $\alpha$ を $x$ の階数(rank)と称する。
次の性質は容易に証明可能できます。
(f) ${\rm~V}_{\alpha}~=~\{x\in{\rm~V}\,|\,{\rm~rank}(x)<\alpha\}$
(g) ${\rm~rank}(x)~=~\sup_{y\in{x}}({\rm~rank}(y)~+~1)$
(h) $\alpha\in{\rm~Ord}~\rightarrow~{\rm~rank}(\alpha)~=~\alpha$
さらにもうひとつ重様な概念である「整順(well founded)な関係」を定義します。
[整順な関係の定義]
集合 $X$ 上の二項関係 $R(x,y)$ が整順(well founded)であるとは次の条件を満たすことである。
$\forall~Y\subset{X}(Y\neq\emptyset~\rightarrow~\exist{y\in{Y}}({\forall{x\in{Y}}}(\neg{R}(x,y))))$
言い替えると $X$ の空でない部分集合に対して $R(x,y)$ の $Y$ に「極小元」が存在するという感じでして、実際定義で現れる $y$ を $Y$ の関係 $R(x,y)$ に対するの極小元と呼ぶのです。さてここで「正則の公理」を導入して、すべての集合が ${\rm~V}$ の要素であることを証明する準備が出来ました。
[正則の公理(axiom of regualarity)]
$\forall{x}(x\neq\emptyset~\rightarrow~\exist{y\in{x}}(y~\cap~x~=~\emptyset))$

[定理]
$\forall{x}\exist{\alpha\in{\rm~Ord}}(x\in{\rm~V}_{\alpha})$
言い替えると
$\forall{x}(x~\in~{\rm~V})$
もっとはっきりと言い替えると
クラス ${\rm~V}$ は集合全体のユニヴァースである！！
正則の公理を「基礎の公理(axiom of foundation)」と呼ぶこともあります。正則の公理の導入により、集合全体がこのように「空集合から巾集合を順序数にそって積み上げ、それを合併の公理により張り合わせる」という集合を拡張する三つの大きな操作、即ち「巾集合の公理」「合併の公理」「置換公理」により美しい形で表現可能であることは驚きであるとともに、現代の集合論の公理の整合性を強く示唆するものであると思うのであります。
さて証明ですが、まず次の事実に注意します。
正則の公理 $\rightarrow$ 任意の集合上で $\in$ は整順な関係。
この事実は「正則の公理」が「任意の集合は $\in$ に関する極小元を持つ」という事実を表現していることに注意すれば明らかです。さらに次の事実に注意します。
$x$ を推移的な集合とするとき $x~\in~{\rm~V}$
これを証明するためには $x\subset{\rm~V}~$ であることを示せば十分です $(x$ の各要素の ${\rm~rank}$ を考える)。実際そうでないとすると、 $y=x-{\rm~V}\neq\emptyset$ となるので $y$ の $\in$ に関する極小元を $z$ として $w\in{z}$ とすします。すると $z$ の極小性により $w\not\in{y}.$ また $x$ の推移性により $w\in{x}.$ したがって $w\in{\rm~V}$ が成立するので $z\subset{\rm~V}$ が成立ち $z\in{\rm~V}.$ これは $y$ の定義に矛盾します。最後に次の事実
$x\in{\rm~V}~\leftrightarrow~{\rm~tc}(x)\in{\rm~V}$
を示せば定理の証明は完了ですが、これは推移的閉包の定義によりほとんど明らかです。

2004年10月9日(土)

藤沢台風情報
現在 15時頃ですが、大分風雨が強まってきました。16時〜17時位がピークになりそうです。
かなり強い雨が降りましたが、あっという間に過ぎ去りました。今は晴れています。

2004年10月8日(金)

ドメイン維持管理請求書
本日アイネットディからおうちのドメイン維持管理代行費用等の請求が来まして、一年分のお値段が 6,300 円なり。いやはや一月 500円と思っているとたいしたことない感じがしますが、一年分となると結構いいお値段ですな。ちなみに、聞いた話によりますと、おうちのドメイン名(evariste.jp) はあまりに神々しいので、その筋の人達の間でも膠着状態になりて、誰もとっていなかったそうで、かなり厚かましい感じがするとのこと。いや〜、こればっかりは変な意図さえなければ早いもの勝ちですから(^^。
X24 と FreeBSD-5 系列
FreeBSD-users-jp のこちらのスレッドによりますと、どうも 5.3-beta で X24 へのインストールに成功した事例があるそうで、いよいよ最新ヴァージョンのの追っかけに移行できそうです。そうはいうものの、最近いまいちコンピューターに対する興味がなくなってきているのと、さらに 4.10 で何の問題もなく動作しているのと移行するのがとっても面倒そうということで、きっと 5.3-release(いつなんだろう)のあたりまでは行動を起こさない様な気がします。ただしいつまでも古いヴァージョンを使っていると、いざというときに困る場合が多いことも経験的に分っているので、ちょいと悩ましいところであったりするのです。
＃ねたがなくて困ったらインストールしようかな...(^^。

2004年10月7日(木)

手に入った「ばらの騎士」
やはり欲しくて色々調べていたのですが、こちらから注文することが出来まして、本日めでたく届いたのです。もちろん定価の 6,500円(+消費税)で手に入った訳で、いやはや先日オークションで負けたのは今になってみれば幸いでした。ところでおうちには DVD を聴く機械は PS2 しかなかったりして、さらに最近はアナログ系がずたぼろでして、音がとぎれたり、画面が変な色になったり、場合によっては垂直同期がとれなくなったりして、しばらくの間は大切にとっとくしかないという悲しい状況だったりします。さらに、お子さま達から新しい PS2 を買ってちょうだい、という圧力も段々高くなっているのが現状なのです(^^。
余談ですが HMV からのメールの形式はあんまり質が良くなく、普通は注文した後にすぐ確認メールが来るのに全然来ないのでどうしたのだろうと思っていたら、全部スパム箱に落ちていたのでした。Spamassassin のポイントは 5.5 で、内訳は次の通りです。「どかん」というよりも「ちびちび」ポイントを稼いでいる感じですな(^^。
```
 pts rule name              description
---- ---------------------- --------------------------------------------------
 0.2 PLING_QUERY            Subject has exclamation mark and question mark
 1.3 GAPPY_SUBJECT          Subject: contains G.a.p.p.y-T.e.x.t
 0.3 NO_REAL_NAME           From: does not include a real name
 0.8 HTML_30_40             BODY: Message is 30% to 40% HTML
 0.7 HTML_TITLE_UNTITLED    BODY: HTML title contains "Untitled"
 0.3 HTML_TAG_BALANCE_BODY  BODY: HTML has unbalanced "body" tags
 0.8 HTML_COMMENT_8BITS     BODY: HTML comment has 3 consecutive 8-bit chars
 0.0 HTML_MESSAGE           BODY: HTML included in message
 1.1 MIME_BASE64_TEXT       RAW: Message text disguised using base64 encoding
```
クラスと V
[集合論雑記目次]
今まで議論してきた様に、例えば「集合全体からなる集合」を考えると矛盾が生じるので、内包に対して外延(集合)を作る場合、公理群によりいろいろな制約を与えてきたのです。ただし「集合全体からなる集まり」「順序数全体からなる集まり」等の概念を考えること自体は便利であるというのは疑いのない事実であり、実際このようは「集まり」を容認する公理系も存在しまして、最も広く使用されているのが「ベルナイス・ゲーデルの公理系(BG 集合論)」であり、集合と考えるには大きすぎる集まりを「真のクラス」と表現して(さらに通常の集合と真のクラスを合わせて「クラス」と称する)、 $C$ が「真のクラス」である特徴づけは次の通りです。
$\forall{x}(C\not\in{x})$
ここで全称記号は真のクラスも含めたクラス全体の領域を動くとします。つまり「真のクラスは別のクラスの要素となることはない」という約束ごとをするのです。
それに反して今までこの雑記で使用してきた公理系は ZF(ツェルメロ・フランケル)集合論と言いまして、集合を作るに際して、「大きくなりすぎない」ように公理で制約を与え、それに反する集まりは「対象として認めない」ものだったのです。さて、本日の目的は ZF 集合論を基礎としつつ、「大きな物の集まり」を考えたいということなのですが、ざっくばらんに例えば「順序数全体の集まり」を考える時に、それを外延化しないで内包のまま考える方式を採用します。例えば順序数全体のクラス、
${\rm~Ord}=\{\alpha|~\alpha~\,\,{\rm~is~ordinal}\}$ (この記法は便宜的なものであり正しい記法ではありません！！)
という「集まり」を考えるつもりになりたいのですが、これは ZF 集合論では許されないので、単に ${\rm~ord}(x)~\leftrightarrow~(x\,\,~{\rm~is~ordinal})$ なる論理式を考えて $\alpha\in{\rm~Ord}$ は単に ${\rm~ord}(\alpha)$ の略記であると考え、さらに上に記述した「正しくない記法」も誤解を招かない限りは採用することとします。
それでは上記の「クラスの定義」を利用して集合のユニヴァース ${\rm~V}$ を定義します。
[V の定義]
${\rm~V}_0~=~\emptyset$
${\rm~V}_{\alpha~+~1}~=~\wp({\rm~V}_\alpha)$
${\rm~V}_{\alpha}~=~\bigcup_{\beta<\alpha}{\rm~V}_{\beta}$ ( $\alpha$ が極限順序数の場合)
として
${\rm~V}~=~\bigcup_{\alpha\in{\rm~Ord}}{\rm~V}_{\alpha}$
最後の ${\rm~V}$ の「定義」はもちろん、
$x\in{{\rm~V}}~\leftrightarrow~\exist{\alpha}(\alpha\,\,{\rm~is~ordinal}\,~\wedge\,~x~\in~{\rm~V}_{\alpha})$
を表現している(しかも左辺は言語の濫用)のであり具体的に ${\rm~V}$ という対象を定義している訳ではありません。それにもかかわらず ${\rm~V}$ を(便宜上)対象と考える直観が役に立つ場合が多いことは事実なのであります。さてすべての集合が ${\rm~V}$ の要素になることは今までの公理からは証明出来ません。この事実を証明するには次回に言及する「正則性の公理」が必要です。

2004年10月6日(水)

ぞうがふんでもでもこわれない

昨日奥さまと話していたら、大昔(私が小学生の頃)の「ぞうがふんでもこわれない」筆入れのコマーシャルの話になったのです。ご存じない方も多いと思いますので、ちょいと説明致しますと、当時の筆入れはセルロイド(これも分んないか^^)製のものが多く、ちょっとした衝撃や圧力で壊れてしまったのです。その時代になんと「ぞうさん」の圧力にも耐えるという筆入れは、子供にとって大変なインパクトがあるコマーシャルだったのであります。

私あれ欲しかったよね

奥さまでも買ってもらえなかった

私私も

奥さま本当に象が踏んでも壊れなかったのかな

私おそらく塩化ビニールかなんかを材質にしてたのでふにゃふにゃして壊れにくかったと思う

奥さま本当に象に踏ませたのかな

私コマーシャルで象に踏ませるところ出てなかったっけ

奥さまよく覚えてない。

私そもそも象の足の裏ってそんなに硬いの？そうでないとすると、踏んだ時象の足の底がへこんで、筆入れにはあんまり圧力がかからないかも...

奥さまじゃあ今度動物園に連れてってあげるから自分で踏まれてみたら(^^

私あのねえ、筆入れの面積は象の足の裏より小さいから、もし象の足の裏が軟らかければ圧力は減少するけど、私が象に踏まれると足全体の重量がかかるからつぶれてしまうよ

奥さまそもそもこの前の写真を見ると象の足の裏硬そうだし

私でも塩化ビニール製だとすると、筆入れは無事でも中の鉛筆とかは壊滅したのでは(^^

実際、当時は物が壊れやすく、頑丈なものに対して子供心にもあこがれがあった時代だったと記憶しております。今だったら「ビルから落としても、象が踏んでも壊れない IBM ノートパソコン」なんてのがあれば 5万円位高くてもふらふら〜、と買ってしまいそうな気がします(^^。

2004年10月5日(火)

怒られないと勉強しない
なんか対偶の話題が出ているようなので...。一般に論理式 $\phi,\,\psi$ に対して $\phi\rightarrow\psi$ の対偶は $\neg\psi\rightarrow\neg\phi$ であることは良く知られた事実であると思います( $\neg$ は否定を表す論理記号)。もう少し分りやすく書くと、
「P ならば Q」の対偶は「Q でないならば P でない」
ということになり、元の命題とその対偶が同値になる事実も良く知られていると思います。すると「怒られないと勉強しない」という言葉に対して一般常識で「対偶」を作ると、
勉強すると怒られる(^^
ということになります。いやはやこれでは勉強する気が失せてしまいます(^^。実際、日常生活では「ならば」ということばや「...でないと」という言葉は頻繁かつ多用途に用いられ、この言葉を直観のおもむくまま形式的な論理に適用すると変な結果を得ることが多々ありうるのです。
さて、上の解釈の問題点を分析しますと、「怒られないと」の部分を「否定文」に解釈することが問題なのであり、これは時制もしくは因果律に関連する文と解釈するべきで、形式論理の規則を適用するためには、「怒られている時は勉強していない」という風に書き直すべきなのです。そして、この言い替えの「対偶」をとると、「勉強しているときは怒られていない」という風に全く問題がない文が出来上るのであります。
ここで本題に入りまして、テナーさんのとこの疑問(2004年10月5日の日記) の「他人は変えることが出来ない」の「対偶」は「他人は変えないことが出来る」であり、後者は明らかに偽であるので最初の文も偽である、ということなのですが、これは「関係」を論理適用する方法の誤りから発生する間違いだと思われます。この場合「他人は」の部分をそのままにしておいて、「変える (変えない)」と「出来る(出来ない)」の部分に「論理規則」を適用することに問題があるのでして、「出来る」という言葉には「何が出来る」かという具体的な条件が記述されていないので、これを一つの論理式(関係)と考えて形式的な論理を適用することが誤りなのです。具体例で言いますと、例えば人間一般を x で表して P(x) を「x は勉強する」という表現に形式論理を応用することが可能であると思われますが、P(x) を「x は出来る」とするとこの表現は意味不明です。つまり、
他人は変えることが (ならば) 出来ない
他人は変えないことが (ならば) 出来る
という「区切り」方と「ならば」の適用に問題がありまして(出来る・出来ないも「ならば」の部分双方が意味不明)、上記の二番目の文に形式論理の「ならば」を無理矢理適用するならば、
他人ならば変えないことが出来る
という感じになるのですが、本当は「他人」という「もの」を表す概念に「ならば」を適用することはやってはいけないので、上の文を論理にあてはめるならば、
x が他人ならば x を変えないことが出来る
と言い替える必要があります。さらに「出来る」という部分はテナーさんがこの文を偽と解釈していることから、「すべの」という意味が言外に含まれていると考えられます。即ちもっときっちり言い替えると、
すべての x に対して (x は他人)かつ(x は変わらない)
となります。そしてその対偶(というかもはや対偶でなく存在に関する言い替え＊)、
「ある x に対し(x は自分)または(x は変わる)」ことはない
となり、これが二番目の文の正しい言い替えであると思うのです。さらに一番目の文を同様に言い替えると、二番目の文と異なりこの文が真であると考えられるからには、言外に「ある」を含むと考えられるので、
ある x に対し(x は他人)かつ(x は変わらない)
となり一番目の文と二番目の文はあんまり関係がなく(少なくとも対偶という意味では)「すべて」もしくは「ある」に関する問題であるということが分るのです。
(＊)論理規則
$\forall{x}(\phi(x)~\wedge~\psi(x))~\,\leftrightarrow~\cr~\neg\exist{x}(\neg(\phi(x)\wedge\psi(x)))~\,\leftrightarrow~\cr~\neg\exist{x}(\neg\phi(x)\vee\neg\psi(x))$
によります。

2004年10月4日(月)

まだ仕事〜
現在丁度未明零時になりましたが、実を言いますとまだ会社で仕事してたりします。まあ「先週中に」という約束なもんで、とにかく朝までに形を整えないと、とってもとってもみっともなかったりするのでした(^^。
今朝の四時半頃ですがなんとか形に(^^。もう限界なのでお客様にプログラムをメールで送りて始発で帰ります(^^。

2004年10月3日(日)

休日出勤
というわけで、今日は一人で会社にいたりするのです(^^。それはそうと、昨日の運動会で「来年入学予定の子供」のかけっこがあったのですが、それを見ていたモカちゃんいわく、
昔この競技に出た時、幼稚園では一番速かったので、当然一番になれると思っていたのが、もっと速い子がいて驚いた
とのことなのです。モカちゃんが通っていた幼稚園は一学年 10人程度のちっちゃいところだったのと、普通の子よりちょっと足が速い、ということでそんな風に思い込んでしまったのでしょうな(^^。それにしてもそんな昔のこと良く覚えていること...。本人にとっては相当な衝撃だったのでしょう。
(おまけ)
写真撮ろうとゴール前に集まるばか親たち

もちろん私もばか親の一人だったりします(^^。

2004年10月2日(土)

運動会
今日は快晴にめぐまれたモカちゃんの運動会でして、100メートル走では一等賞だったのでした(^^。なんか写真を出したいところですが、そろろろ姫もおっきくなってきたのと、今日はあんまり良いのが撮れなかった(というか他の子が写っている)のです。仕方ないので、先週奥さまとモカと二女が上野動物園に行ってきた時、二女とモカが撮った写真掲載なのです(^^。動物園に行ってきたのは先週の日曜日でして、私も行こうと思ったのですが、猫森疲れで朝起きれなかったというなんとも情けない父親なのです。

2004年10月1日(金)

今日から十月
なんか全く意味のない題名だったりします。ところで大分気候も良くなってきて、そちらは助かるのですが、いよいよ仕事が切羽詰まってきたりしています(^^。うーん、明日はとある行事があるので仕事出来ないし、これは日曜日に出勤するしかなさそうですが、先々週あたりからのイベント疲れも残っていたりして、ちょいとつらいところです。まあ来週の中ごろには落ち着くと思いますので、そしたら日曜日の代休でもとって家でごろごろして過ごしましょう(^^。それから最近集合論雑記の更新が止まってしまっています。こちらもそろそろなんとかしなくてはいけません。
＃仕事も行き詰まっているのではなく、単に面倒な部分をこつこつやれば良い
＃状況なので案外気楽なのでした(^^。

2004年7月6日から 18346 アクセス

2004年9月 2004年11月更新履歴と日記の先頭に戻る日記の目次
 集合論雑記目次
 はてなリング数学の輪
 トップページに戻る谷山浩子さんのページ

私	あれ欲しかったよね
奥さま	でも買ってもらえなかった
私	私も
奥さま	本当に象が踏んでも壊れなかったのかな
私	おそらく塩化ビニールかなんかを材質にしてたのでふにゃふにゃして壊れにくかったと思う
奥さま	本当に象に踏ませたのかな
私	コマーシャルで象に踏ませるところ出てなかったっけ
奥さま	よく覚えてない。
私	そもそも象の足の裏ってそんなに硬いの？そうでないとすると、踏んだ時象の足の底がへこんで、筆入れにはあんまり圧力がかからないかも...
奥さま	じゃあ今度動物園に連れてってあげるから自分で踏まれてみたら(^^
私	あのねえ、筆入れの面積は象の足の裏より小さいから、もし象の足の裏が軟らかければ圧力は減少するけど、私が象に踏まれると足全体の重量がかかるからつぶれてしまうよ
奥さま	そもそもこの前の写真を見ると象の足の裏硬そうだし
私	でも塩化ビニール製だとすると、筆入れは無事でも中の鉛筆とかは壊滅したのでは(^^